Бинарная арифметика (первая часть)
15 августа 2024 г.Пролог (оффтоп)
Второго августа 2023-го года, в снапшоте 23w31a в Minecraft появились макросы функций, которые позволяли вызывать функции в датапаках с аргументами так, как это делалось бы в нормальном языке программирования. И мне всегда хотелось чтобы у датапаков был высокоуровневый язык программирования, такой как mcscript (но только до сих пор поддерживаемый) или CBScript (но только с документацией). Я, может, и не был бы тем, кто стал бы этим заниматься, но обновление все равно вдохновило меня сделать хоть что-нибудь.
Тогда же я узнал про датапак gm. Он был именно тем, чем себя заявлял — набором служебных функций для работы с числами с плавающей точкой, которую Minecraft не поддерживает по-умолчанию: хотя в нем можно выполнять операции над целыми числами через /scoreboard, то же самое делать с дробными не получится. В датапаке числа хранились в формате чем-то напоминающим стандартную запись, как объект со следующими параметрами:
decдля позиции точки относительно наименее важной цифры (целое число)polдля знака (целое число, 1 или -1)baseдля основания системы счисления (целое число)numдля цифр (массив целых чисел)
В таком формате число 3.14159 хранилось бы как
{
"dec" : 5,
"pol" : 1,
"base" : 10,
"num" : [3, 1, 4, 1, 5, 9]
}
Когда я начал играться с датапаком, я обнаружил, что функция деления у него не работает как следует. Я открыл ишью on github и в конце концов ее закрыли как "not planned". Ну что же. Придется делать все самому. К сожалению, однако, я тогда очень мало знал про бинарную арифметику, далеко не достаточно чтобы что-то писать, и когда я попробовал разобраться, то она оказалось едва-едва слишком сложной для меня. Прошел год, и я думаю, пора. Но прежде чем я занялся бы дробными числами, надо узнать про целые так много, как получится.
Двоичный код
В этой серии постов я буду предполагать, что читатель знаком с тем, как двоичные числа хранятся в памяти. Но если вдруг он не знаком, то я постараюсь как умею объяснить это здесь.
Пусть у нас, скажем, есть число 135. Нам легко его прочесть, не думая мы видим что это сто и еще что-то — потому что у него три цифры и первая из них это 1. Потом мы видим, что это на самом деле сто и тридцать пять: тридцать потому что вторая цифра это 3, пять потому что третья — 5. Даже в нашей голове мы думаем о числе как о сумме цифр, каждая из которых умножена на какую-то степень десяти — 1 на 100, 3 на 10, 5 на 1. То есть, 1*10^2 + 3*10^1 + 5*10^0.
- 135 это 5 * 10^0, то есть 5
- 135 это 3 * 10^1, то есть 30
- 135 это 1 * 10^2, то есть 100
Это число, 10, степени которого мы используем для представления других чисел; 10, которое мы можем написать только как один и ноль, есть основание десятичной системы счисления. Но это абсолютно произвольное число. В истории существовали системы счисления с другими основаниями, просто так вышло, что десятичная используется сегодня намного больше всех остальных.
Но вместо десятки может быть и двойка. И если в десятичной системе мы используем цифры от 0 до 9, то в двоичной мы бы использовали только 0 и 1. В десятичной мы имеем десять цифр от нуля до десяти, но у нас нет цифры для самой десятки, потому что десять это основание; аналогично, в двоичной нет цифры для двойки, есть только ноль и единица. В двоичной мы бы считали от 0, потом до 1, потом сразу до 10, то есть до двух. Потому что как бы мы еще записали двойку? Как "2"? Мы не можем использовать "2". Цифры от 2 до 9 недоступны. Поэтому это будет 10. Цифра, которая может быть только единицей или нулем, называется бит.
Как я говорил раньше, число в десятичной системе это сумма произведений цифр на степени двойки. 42 это 4*10^1 + 2*10^0. То же справедливо и для двоичной, но вместо степеней десяти мы используем степени двойки. Взглянем на число 11010, к примеру:
- 11010 это 0 * 2^0, то есть 0
- 11010 это 1 * 2^1, то есть 2
- 11010 это 0 * 2^2, то есть 0
- 11010 это 1 * 2^3, то есть 8
- 11010 это 1 * 2^4, то есть 16
Сложив это все вместе, мы получаем 26. Следовательно, 110102 = 2610.
Еще стоит заметить что обычно компьютеры хранят числа как ограниченный набор бит (длина это обычно тоже степень двойки — 8, 16, 32 или 64). И если само число имеет меньше цифр, чем ему позволено, то оставшиеся заполняются нулями. Поэтому если бы мы хотели хранить 26 как восьмибитное целое число, то мы бы записывали его как 00011010. Первый бит (самый левый) называется старший бит (или наиболее значимый бит), потому что он важнее всего для числа. Например, есть ощутимая разница между числами 100110102 и 000110102, в то время как 000110112 и 000110102 отличаются друг от друга только на единицу.
Сложение, полусумматор, полный сумматор
Сложение двух десятичных чисел это тоже интуитивный процесс, особенно если везет и ни одна из сумм пар цифр не превышает десять. Допустим, мы складываем 1224 и 3163:
1224
+ 3163
------
4387
Очень просто, да? Мы двигаемся от младшей цифры к старшей, складываем две цифры от каждого числа и записываем результат на их место. И если сумма двух цифр больше десяти, то тут тоже не слишком сложно: мы просто переносим единицу в следующую позицию, прибавляя и её тоже.
--1- |
1228 | 8
+ 3163 | + 3
--------+-----
4391 | 11
В двоичной системе все еще проще, да настолько, что все двоичное сложение можно описать как набор логических гейтов. Соорудим-ка цепь, которая складывает две цифры, A и B. Поскольку каждая из них это бит, существует только четыре возможных пары их значений: [0, 0]; [0, 1]; [1, 0]; [1, 1].
Для [0, 0] сумма была бы 0. Для [0, 1] и [1, 0] сумма была бы 1. Но поскольку в двоичной системе 1 + 1 это 10, сумма [1, 1] была бы 0. А куда нам перенести единичку? Если у цепи только один вывод, бит суммы, то некуда. Поэтому нам нужен второй бит — бит (или флаг) переноса. Для [0, 0], [0, 1] и [1, 0] он был бы равен 0, поскольку у нас никакого переполнения не происходит. Но для [1, 1] он был бы равен единице, потому что нам есть, что переносить в следующую позицию. Таблица истины для такой цепи выглядела бы вот так:
A | B | Перенос | Сумма
---+---+---------+-------
0 | 0 | 0 | 0
---+---+---------+-------
1 | 0 | 0 | 1
---+---+---------+-------
0 | 1 | 0 | 1
---+---+---------+-------
1 | 1 | 1 | 0
Взглянув на эту таблицу, видно, что бит суммы это просто XOR от A и B, а бит переноса — AND. Эта цепь называется полусумматор. Но она, к сожалению, не может самостоятельно выполнять сложение целиком: у нас может и есть бит переноса, но мы с ним ничего не делаем, а у полусумматора его некуда воткнуть — соответственно, передавать переполнение вперед по цифрам мы не можем. Для этого нам нужен полный сумматор. Его единственное отличие в том, что кроме входов A и B у него еще есть бит входящего переноса. Его таблица истинности выглядит так:
A | B | Carry-in | Carry-out | Сумма
---+---+----------+-----------+-------
0 | 0 | 0 | 0 | 0
---+---+----------+-----------+-----
1 | 0 | 0 | 0 | 1
---+---+----------+-----------+-----
0 | 1 | 0 | 0 | 1
---+---+----------+-----------+-----
1 | 1 | 0 | 1 | 0
---+---+----------+-----------+-----
0 | 0 | 1 | 0 | 1
---+---+----------+-----------+-----
1 | 0 | 1 | 1 | 0
---+---+----------+-----------+-----
0 | 1 | 1 | 1 | 0
---+---+----------+-----------+-----
1 | 1 | 1 | 1 | 1
Carry-in тут это входящий бит переноса, carry-out — выходящий
Выглядит намного более сложно чем полусумматора, но полный сумматор можно сделать из двух полусумматоров и гейта OR, расположенных таким образом:
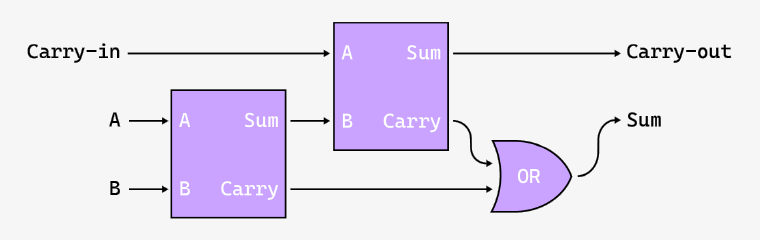
С полным сумматором мы можем направить выходящий бит переноса к входящему у следующего полного сумматора. Таким образом, чем больше в цепи сумматоров, тем длиннее числа мы можем складывать.
Вычитание и дополнительный код
Интуитивно можно предположить, что в мире, где полусумматоры и полные сумматоры используются для сложения, для вычитания используются полувычитаторы с полными вычитаторами. И это не совсем неправда: полувычитатели и полные вычитатели существуют и спокойно гуглятся. Но когда речь идет об операциях над целыми числами со знаком намного чаще для вычитания используется нечто под названием дополнительный код (англ. "two's complement"): специальный способ представления отрицательного числа в двоичной системе таким образом, что при сложении его с другим числом используя сумматоры происходило бы вычитание. "Дополнительный код числа X" есть отрицательное значение X, закодированное таким образом.
Прямолинейным подходом для записи целых чисел со знаком в памяти было бы зарезервировать один бит (старший бит) как бит знака: если старший бит равен нулю, то число положительное, а если одному, то отрицательное. Таким образом 00001101 было бы 13, а 10001101 было бы -13. Дополнительный код похож на это в том плане, что старший бит таким же образом отвечает за знак числа, но остальная часть числа читается по-разному в зависимости от того, положительное ли оно или отрицательное.
Чтобы вычислить дополнительный код числа, надо инвертировать все его биты и прибавить единичку. Так что дополнительный код 13, то есть, 00001101, был бы 11110011. Инвертируя 00001101, мы получаем 11110010, а прибавляя к этому единицу — 11110011. Это -13 в дополнительном коде. А теперь магия: если бы мы захотели вычесть 13 из, скажем, 34, то это было бы то же самое, что и добавить 11110011 к 00100010:
00100010
+ 11110011
----------
100010101
У нас получилось 100010101, но поскольку у нас есть только восемь бит на одно число, старший бит — единичку — нам придется отбросить, что даст нам 00010101. По удивительному совпадению, это 21 в двоичной системе, то есть разность 34 и 13. И вот почему это работает:
Поскольку мы используем числа фиксированной длины, мы можем воспользоваться тем, что для числа длиной в N бит добавление 2^N равносильно добавлению 0 из-за переполнения. Для восьмибитных чисел, прибавление 2^8, то есть 100000000, ничего не сделает, потому что нам придется избавиться от девятого бита после сложения, а все остальные биты остаются неизменными. На этом построен механизм работы дополнительного кода: мы можем вычесть число из 2^N и потом прибавлять результат к чему угодно, относясь к нему как к отрицательному значению этого числа. Если мы вычтем X из 100000000 и прибавим разность к Y, то это будет все равно что вычесть X из Y.
Последнее, что стоит сказать, это то, почему работает фокус с инвертированием битов и прибавлением единички: так вышло, что вычитать N-битное число из 2^N требовало бы N + 1 бит для хранения 2^N. Это совершенно неэффективно с аппаратной точки зрения. Вместо этого мы можем вычесть число из (2^N - 1) и прибавить единичку когда-нибудь потом. И вот в чем фокус: (2^N - 1) это просто бит 1 повторенный N раз. (2^8 - 1) это 11111111, (2^16) это 1111111111111111, так далее. И вычитать бит из единицы это все равно что инвертировать его: 1 - 0 это 1, 1 - 1 это 0. Так что вычесть число из (2^N - 1) это все равно что инвертировать его, а вычесть число из 2^N это все равно что инвертировать его и прибавить единичку.
Поэтому чтобы вычесть B из A с помощью дополнительного кода, делуется следующее:
- Инвертируется каждый бит в B.
- К B добавляется единица.
- B добавляется к A.
A: 00100010, B: 00001101
1. Инвертируем каждый бит в B.
B: 00001101 -> 11110010
2. Добавляем 1 к B.
11110010
+ 00000001
----------
11110011
3. Добавляем B к A.
00100010
+ 11110011
----------
100010101
Result: 00010101
Вот и все, что касается сложения и вычитания. На очереди — умножение, сразу после рекламы.