Возвращаясь к основам растеризации

Какое-то время я проводил небольшие занятия по программированию для детей в лагере пока мне было шестнадцать. На одном из таких я написал на C# программу которая отображает аналоговые часы в окне консоли. Некоторых детей это даже немного впечатлило. Программа состояла из двух частей: одна рендерит сами часы в двумерный массив ASCII символов (фреймбуфер, если угодно), другая выводила его в окно и изменяла его размер если менялся размер окна.

Мне очень сильно хотелось порассказывать о компьютерной графике и растеризации, но растеризация полигонов тогда для меня самого не была совсем понятна, поэтому я решил остановиться на чем-нибудь проще. Стрелки часов рендерились бы алгоритмом для отрисовки прямых линий, циферблат — алгоритмом для отрисовки окружностей — тогда это казалось очень хорошей идеей.

Несколько недель назад я решил вернуться к ней и попробовать переписать эти часы без гугла, опираясь на те знания, которые у меня остались спустя это время. Алгоритмы, которые у меня получились в итоге, лучше всего описать как "наивные".

Отрисовка линий

Для прямых линий я остановился на самом простом и прямолинейном подходе, который не требовал бы сортировки точек. Для такой простой программы, я считаю, это не критично, потому что мы всегда рисуем только три линии за кадр и едва ли говорим о каком-то высоком разрешении.

1. Сначала вычислить разность между координатами двух точек. Эту разность мы запишем в delta_x и delta_y.
2. После этого найти наибольшее из двух модулей (абсолютных величин) разностей. Это будет количество пикселей, которые надо отрисовать. Запишем в steps.
3. Разделить delta_x и delta_y на steps и записать частные в increment_x и increment_y. Оставшееся должно быть довольно очевидным.
4. Скопировать start_x и start_y в x и y, записать 0 в переменную i.
5. Отрисовать символ на x и y.
6. Прибавить increment_x и increment_y к x и y, прибавить 1 к i.
7. Если i меньше чем steps, то перейти к шагу №5.

Если перенести это на код, то получится что-то вроде следующего:

void DrawLine(double start_x, double start_y, double end_x, double end_y, char c)
{
    double delta_x = end_x - start_x;
    double delta_y = end_y - start_y;

    // Не сильно горжусь этой частью
    int steps = (int)Math.Round(
        Math.Max(
            Math.Abs(delta_x), 
            Math.Abs(delta_y)
            )
        );

    double increment_x = delta_x / steps;
    double increment_y = delta_y / steps;

    double x = start_x;
    double y = start_y;

    for (int i = 0; i <= steps; i++)
    {

        DrawPixel(x, y, c);
        x += increment_x;
        y += increment_y;
    }
}

Отрисовка окружностей

Здесь идея несколько другая: перебрать каждый x, принадлежащий окружности, и для каждого x найти два соответствующих y. Я решил работать от (x - O.x)^2 + (y - O.y)^2 = r^2, где O это центр окружности и r это радиус. Переписав этот для y, я получил y = O.y ± sqrt( r^2 - (x - O.x)^2 ). Этого мало, однако, потому что у растеризованной окружности есть участки, где на одну координату x приходится несколько пикселей с разными y (и наоборот).

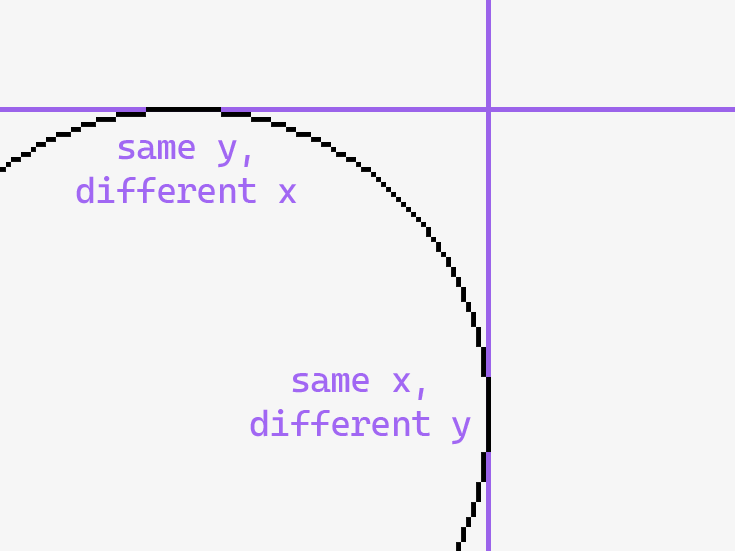
If we only solve for one coordinate iterating through the other one, we'll get artifacts that look like this:

Если мы найдем значения только одной из двух координат от значения другой, то мы получим такие артефакты:

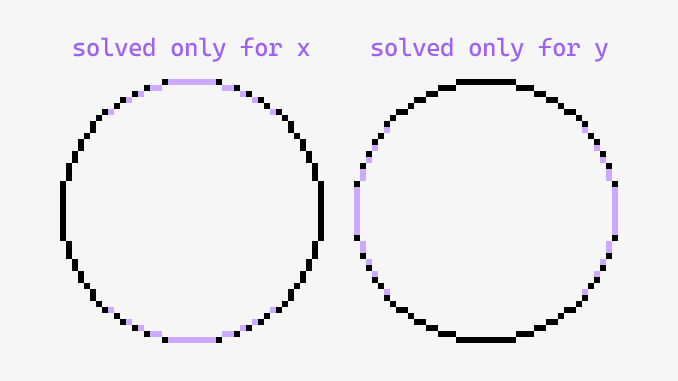
Поэтому, помимо перебора каждого x и вычисления O.y ± sqrt( r^2 - (x - O.x)^2 ) для y, мы должны перебрать каждый y и вычислить O.x ± sqrt( r^2 - (y - O.y)^2 ) для x. Это приведет к тому, что две функции наложатся друг на друга, и поэтому если раньше мы допускали перебор каждого x который удовлетворяет O.x - r < x < O.x + r (и так же для y), то мы можем избавиться от наслоения если ограничим x до O.x - r * sqrt(2) < x < O.x + r * sqrt(2).

Но это только если мы говорим об отрисовке обыкновенного круга. К сожалению, на самом деле

Отрисовка растянутых окружностей

Соотношение сторон моноширного символа обычно что-то около 2:1, и поэтому соотношение сторон "пикселей" у наших часов будет такое же. И хотя это не влияет на то, как мы отрисовывали бы линии, окружности из-за этого придется рисовать дважды шире обычных, сохраняя их высоту. Изменить функции чтобы учитывать это работая с C# было бы неоправданно тяжело для меня, поэтому я использовал https://www.desmos.com/ для того, чтобы смоделировать программу и найти выражения, которые мне нужны. Они получились следующие:

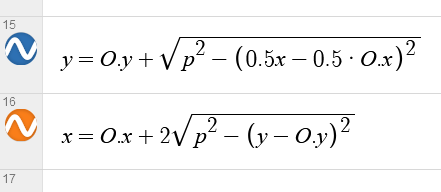
Маленькая модель, которая у меня получилась, доступна тут, но там в большей степени про то, о чем я и так до этого говорил. Переведя эти измененные выражения в C#, я получил следующий код:

void DrawCircle(double origin_x, double origin_y, double radius, char c)
{
    double leftmost_x = origin_x - radius * Math.Sqrt(2);
    double rightmost_x = origin_x + radius * Math.Sqrt(2);

    double topmost_y = origin_y - radius * Math.Sqrt(0.5);
    double bottommost = origin_y + radius * Math.Sqrt(0.5);

    for (double x = leftmost_x; x < rightmost_x; x++)
    {
        DrawPixel(
            x,
            origin_y + Math.Sqrt(radius * radius - Math.Pow(0.5 * x - 0.5 * origin_x, 2)),
            c
        );

        DrawPixel(
            x,
            origin_y - Math.Sqrt(radius * radius - Math.Pow(0.5 * x - 0.5 * origin_x, 2)),
            c
        );
    }

    for (double y = topmost_y; y < bottommost; y++)
    {
        DrawPixel(
            origin_x + 2 * Math.Sqrt(radius * radius - Math.Pow(y - origin_y, 2)),
            y,
            c
        );

        DrawPixel(
            origin_x - 2 * Math.Sqrt(radius * radius - Math.Pow(y - origin_y, 2)),
            y,
            c
        );
    }
}

Тут видно, что вырвиглазные вызовы DrawPixel() это всего лишь немного запутанные выражения. Я не знаю, как это сделать без математики, к сожалению. Напишите мне, если у Вас есть идеи.

Заключение

Хотя я думаю, я хорошо постарался с отрисовкой окружностей, алгоритм отрисовки линий оставляет желать лучшего. Теперь я думаю о том, чтобы почитать побольше про алгоритм Брезенхема и про то, что известно как алгоритм DDA-линии. Я, вероятно, почитаю что-нибудь про сглаживание когда-нибудь.

Рассчитывайте на обновления программы в недалеком будущем.